邱奇数的C++实现

邱奇数(Church Numerals)是 $\lambda$ 演算中的一个著名例子。我们可以通过实现它来了解和练习使用C++14里的Generic Lambda。本文里的例子最新的C++编译器（VC2015, g++ 6, clang++ 3.8）都可以编译运行。

什么是邱奇数？

邱奇数是通过函数来表示自然数的方法。直观上讲，邱奇数可以类比于下图（图一）里表示数字的方法。假设我们有一个球，我们可以把这个球放到一个箱子里，然后可以把这个装着球的箱子再放到另一个箱子里，依次类推。当然你也可以用俄罗斯套娃来想象这个过程。当只有球的时候，我们说这种情况代表0；当有一个箱子的时候代表1。这样我们就可以用嵌套的箱子的个数来代表自然数了。

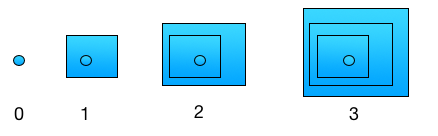
邱奇数的构建过程是很类似的。设有一个自变量 $x$ 和一个函数 $f$，单独的 $x$ 表示0; 当函数作用一次时，我们得到 $f(x)$，我们以此代表1。类似的，数字2就是这个函数作用两次，即 $f(f(x))$。更普遍的，给定自然数 $n$, 其对应的邱奇数就是把 $f$ 作用 $n$ 次。如果我们要用程序语言来实现邱奇数，那么这个程序语言必须支持高阶函数（Higher Order Functions）。所谓的高阶函数就是可以接受别函数的函数，也可以返回一个函数。要实现高阶函数，函数必须可以可以被当成一个值来传递。为什么必须要求高阶函数呢？这是因为邱奇数本质上就是函数，作用在邱奇数上的代数操作必然是处理函数，产生函数的函数。

C++中的lambda

C++14标准里的Generic Lambda是一种函数，它可以当作值传递，接受别的lambda表达式作为参数，并且可以返回一个lambda表达式。它最基本的形式是：

1 2	auto n = 1; auto square = [n] (auto x) {return (x + n) * (n + x);};

这里我们定义了一个变量square，它的值是一个lambda表达式。一个lambda表达式包含三个部分：

捕获列表：定义一个lambda时，我们有时候希望能用到定义这个lambda时所在的环境里的其他变量或者值。我们可以把这些放到捕获列表里，比如这里的$n$。除了通过值捕获，我们还可以通过引用（reference）来捕获，其形式是[&n]。
参数列表：和普通函数一样，表示函数的变量。
函数体：函数的实现代码。如果没有return语句，函数返回类型是void。

更加详细的描述可以参照这里。

邱奇数的lambda表达式

用lambda来表述，每一个数都是一个高阶函数，比如0对应的邱奇数：

1
2
3

auto zero = [](auto f) { 
    return [=](auto x) { 
        return x;};};

如前所述，邱奇数是通过一个变量 $x$ 和一个函数 $f$ 来定义的。所以它必然需要两个参数。在这里我们用了两个嵌套的函数来表达。注意在内层的lambda表达式里我们把=放到捕获列表里了，它的意思是把这个函数所在的环境里的所有变量的值捕获到内部的lambda表达式里。因为这个环境里只有 $f$，所以[=]等同于[f]。除了捕获变量的值，我们也可以捕获变量的引用，即使用[&]。值得注意的是，调用这个函数的时候如果只提供一个参数，例如zero("Hey")，它会返回一个函数而不是值。我们也可以直接提供两个参数，例如zero("Hey")("Jude")，它的返回值是Jude。

对0来说，我们没有作用 $f$ 到 $x$ 上。那么我们怎么来表示1呢。我们把 $f$ 作用在 $x$ 上一次，像这样：

1
2
3

auto one = [](auto f) { 
    return [=](auto x) { 
        return f(x);};};

⚠️这里 $f$ 必须是一个函数，因为在内部的lambda里我们把 $x$ 作为变量传给了 $f$。

当然我们不可能像这样把每一个自然数都写出来，所以我们需要更加普遍的方法来构造邱奇数。最基本的一个操作就是给一个数加一：

auto add1 = [](auto n) { 
    return [=](auto f) { 
        return [=](auto x) { 
            return f(n(f)(x));};};};

add1是一个典型的高阶函数。它接受一个邱奇数，返回一个新的邱奇数。在这里，我们把 $f$ 作用在 $n$ 上，根据邱奇数的定义，它表示 $n + 1$。有了这个函数，我们就可以从0开始不断的加一产生一系列的数。比如：

1 2	auto one = add1(zero); auto two = add1(one);

从add1我们可以看出，给一个数加一，就是把 $f$ 作用在其上。很自然的，我们可以把两个数相加：

auto add = [](auto m, auto n) {
    return [=](auto f) {
        return [=] (auto x) {
           return m(f)(n(f)(x));};};};

可以看到，$m + n$ 就是把 $n$ 作为值传递给 $m$。因为 $n$ 已经把 $f$ 应用了 $n$ 次，如果把 $n$ 作为 $m$ 的变量，$m$ 就会把 $f$ 作用到 $n$ 上 $m$ 次，这样我们总计应用了 $m + n$ 次。例子：

1	auto three = add(one, two);

邱奇数到自然数的转化

既然邱奇数是自然数的一种表达方式，那么我们应该可以把邱奇数转化成自然数。另一个好处，把邱奇数转化成自然数也可以验证我们的代码是否正确。因为邱奇数对应的自然数就是应用 $f$ 到 $x$ 上的次数，选择适当的 $f$ 和 $x$ 就可以达到我们的目的。显然如果我们选择 $x = 0$ 作为初始值，而 $f$ 每次的调用都返回 $x + 1$，最终的返回值就是 $f$ 被调用的次数。所以我们可以定义：

1	auto convert = [](auto x) {return x + 1;};

转化的方法就是把convert传递给一个邱奇数：

1	auto n = three(convert)(0);

我们也可以通过邱奇数来多次调用一个函数，比如打印一个字符串3次：

1 2	auto says = [] (auto x) {std::cout << x << std::endl; return x;}; three(says)("Hello from 3");

⚠️邱奇数里的函数 $f$ 必须接受一个值，并且返回一个同类型的值。

结束语

以上的所有代码都可以在这里获取。我们仅仅实现了最基本的几个关于邱奇数的函数。开动脑洞，我们也可以做许多很有趣的事情。比如这里，作者用Ruby里的lambda函数实现了FizzBuzz。