Posted on

邱奇数(Church Numerals)是 $\lambda$ 演算中的一个著名例子。我们可以通过实现它来了解和练习使用C++14里的Generic Lambda。本文里的例子最新的C++编译器（VC2015, g++ 6, clang++ 3.8）都可以编译运行。

什么是邱奇数？

邱奇数是通过函数来表示自然数的方法。直观上讲，邱奇数可以类比于下图（图一）里表示数字的方法。假设我们有一个球，我们可以把这个球放到一个箱子里，然后可以把这个装着球的箱子再放到另一个箱子里，依次类推。当然你也可以用俄罗斯套娃来想象这个过程。当只有球的时候，我们说这种情况代表0；当有一个箱子的时候代表1。这样我们就可以用嵌套的箱子的个数来代表自然数了。

图一

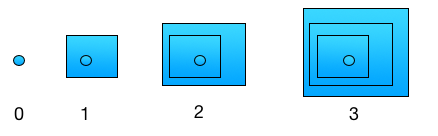
邱奇数的构建过程是很类似的。设有一个自变量 $x$ 和一个函数 $f$，单独的 $x$ 表示0; 当函数作用一次时，我们得到 $f(x)$，我们以此代表1。类似的，数字2就是这个函数作用两次，即 $f(f(x))$。更普遍的，给定自然数 $n$, 其对应的邱奇数就是把 $f$ 作用 $n$ 次。如果我们要用程序语言来实现邱奇数，那么这个程序语言必须支持高阶函数（Higher Order Functions）。所谓的高阶函数就是可以接受别函数的函数，也可以返回一个函数。要实现高阶函数，函数必须可以可以被当成一个值来传递。为什么必须要求高阶函数呢？这是因为邱奇数本质上就是函数，作用在邱奇数上的代数操作必然是处理函数，产生函数的函数。

C++中的lambda

C++14标准里的Generic Lambda是一种函数，它可以当作值传递，接受别的lambda表达式作为参数，并且可以返回一个lambda表达式。它最基本的形式是：

1
2
auto n = 1;
auto square = [n] (auto x) {return (x + n) * (n + x);};

这里我们定义了一个变量square，它的值是一个lambda表达式。一个lambda表达式包含三个部分：

  • 捕获列表：定义一个lambda时，我们有时候希望能用到定义这个lambda时所在的环境里的其他变量或者值。我们可以把这些放到捕获列表里，比如这里的$n$。除了通过值捕获，我们还可以通过引用（reference）来捕获，其形式是[&n]。
  • 参数列表：和普通函数一样，表示函数的变量。
  • 函数体：函数的实现代码。如果没有return语句，函数返回类型是void。

更加详细的描述可以参照这里。

邱奇数的lambda表达式

用lambda来表述，每一个数都是一个高阶函数，比如0对应的邱奇数：

1
2
3
auto zero = [](auto f) { 
    return [=](auto x) { 
        return x;};};

如前所述，邱奇数是通过一个变量 $x$ 和一个函数 $f$ 来定义的。所以它必然需要两个参数。在这里我们用了两个嵌套的函数来表达。注意在内层的lambda表达式里我们把=放到捕获列表里了，它的意思是把这个函数所在的环境里的所有变量的值捕获到内部的lambda表达式里。因为这个环境里只有 $f$，所以[=]等同于[f]。除了捕获变量的值，我们也可以捕获变量的引用，即使用[&]。值得注意的是，调用这个函数的时候如果只提供一个参数，例如zero("Hey")，它会返回一个函数而不是值。我们也可以直接提供两个参数，例如zero("Hey")("Jude")，它的返回值是Jude。

对0来说，我们没有作用 $f$ 到 $x$ 上。那么我们怎么来表示1呢。我们把 $f$ 作用在 $x$ 上一次，像这样：

1
2
3
auto one = [](auto f) { 
    return [=](auto x) { 
        return f(x);};};

⚠️这里 $f$ 必须是一个函数，因为在内部的lambda里我们把 $x$ 作为变量传给了 $f$。

当然我们不可能像这样把每一个自然数都写出来，所以我们需要更加普遍的方法来构造邱奇数。最基本的一个操作就是给一个数加一：

1
2
3
4
auto add1 = [](auto n) { 
    return [=](auto f) { 
        return [=](auto x) { 
            return f(n(f)(x));};};};

add1是一个典型的高阶函数。它接受一个邱奇数，返回一个新的邱奇数。在这里，我们把 $f$ 作用在 $n$ 上，根据邱奇数的定义，它表示 $n + 1$。有了这个函数，我们就可以从0开始不断的加一产生一系列的数。比如：

1
2
auto one = add1(zero);
auto two = add1(one);

从add1我们可以看出，给一个数加一，就是把 $f$ 作用在其上。很自然的，我们可以把两个数相加：

1
2
3
4
auto add = [](auto m, auto n) {
    return [=](auto f) {
        return [=] (auto x) {
           return m(f)(n(f)(x));};};};

可以看到，$m + n$ 就是把 $n$ 作为值传递给 $m$。因为 $n$ 已经把 $f$ 应用了 $n$ 次，如果把 $n$ 作为 $m$ 的变量，$m$ 就会把 $f$ 作用到 $n$ 上 $m$ 次，这样我们总计应用了 $m + n$ 次。例子：

1
auto three = add(one, two);

邱奇数到自然数的转化

既然邱奇数是自然数的一种表达方式，那么我们应该可以把邱奇数转化成自然数。另一个好处，把邱奇数转化成自然数也可以验证我们的代码是否正确。因为邱奇数对应的自然数就是应用 $f$ 到 $x$ 上的次数，选择适当的 $f$ 和 $x$ 就可以达到我们的目的。显然如果我们选择 $x = 0$ 作为初始值，而 $f$ 每次的调用都返回 $x + 1$，最终的返回值就是 $f$ 被调用的次数。所以我们可以定义：

1
auto convert = [](auto x) {return x + 1;};

转化的方法就是把convert传递给一个邱奇数：

1
auto n = three(convert)(0);

我们也可以通过邱奇数来多次调用一个函数，比如打印一个字符串3次：

1
2
auto says = [] (auto x) {std::cout << x << std::endl; return x;};
three(says)("Hello from 3");

⚠️邱奇数里的函数 $f$ 必须接受一个值，并且返回一个同类型的值。

结束语

以上的所有代码都可以在这里获取。我们仅仅实现了最基本的几个关于邱奇数的函数。开动脑洞，我们也可以做许多很有趣的事情。比如这里，作者用Ruby里的lambda函数实现了FizzBuzz。

Posted on

Recently I decided to pick up probability theory again. This is a subject that always puzzles me. One thing I noticed is that sometimes the notations used in probability theory can be quite misleading. In contrast, a programming language is meant to be precise on what it says. So can we express concepts in probability theory using some programming language constructs so that one can understand them better? This post is such an attempt.

Modern probability theory is based on the concept of Sets. A probability space consists a set $\Omega$, a probability function $P$ that maps a subset (event) of $\Omega$ to a real number. (To be complete, it also includes a $\sigma$-algebra of subsets of $\Omega$ which I will not talk about.) The probability function $P$ satisfies two properties:

  1. $P(\emptyset) = 0, P(\Omega) = 1$
  2. If $A_1, A_2, \dots$ satisfy $A_i\cap A_j = \emptyset$ when $i \ne j$, we have
    $$P(\cup A_i) = \sum P(A_i)$$

As in any complex system, we have (see SICP for an excellent introduction)

  • Some primitive building blocks, e.g., elements of a set.
  • Ways of combining primitive building block to form more complex object, e.g., forming of subsets, and union and intersection of sets

It is thus very important to understand to how to combine events to form new events. However, I found that the operator $\cap$ is often so heavily overloaded that its usage can be quite confusing. In set theory, $A\cap B$ means a new subset where $x \in A$ and $x \in B$ must both be true for any element $x$ of it. But in probability theory, it means both event $A$ and event $B$ occur in an experiment. This can mean the same thing as in set theory. But it can also mean quite different thing, namely a Cartesian product formed from two different sets, e.g., the definition of independency of events: $P(A\cap B) = P(A)P(B)$. If you think of $\cap$ as intersection of $A$ and $B$, this will never happen.

Tossing dice

We can use types in OCaml to experiment and clarify these concepts. Let’s use dice as an example. We can define dice as follows,

1
2
3
4
5
6
7
8
9
10
type 'a toss =
  | One   of 'a
  | Two   of 'a
  | Three of 'a
  | Four  of 'a
  | Five  of 'a
  | Six   of 'a
type fair_dice   = Fair_dice
type biased_dice = Biased_dice

To be more general, let’s assume there are two types of dice, namely, fair dice and biased dice. For any dice, there are 6 outcomes of tossing it. These 6 outcomes are the primitive elements of the probability space. We can represent such an element as Five(Biased_dice), which means that we toss the fair dice and get a Five. If we type it in the REPL, we have

1
2
let five = Five(Biased_dice);;
(* val five : biased_dice toss = Five Biased_dice *)

Note the type of five is biased_dice toss. How nice it is! Now following the definition of probability space, we need to define a function that assign a number to each set element.

1
2
3
4
5
6
7
8
9
10
11
12
13
let prob_fair_elem x =
  match x with
  | One(Fair_dice) -> 1.0 /. 6.0
  | _              -> 1.0 /. 6.0
let prob_biased_elem x =
  match x with
  | One(Biased_dice)   -> 1.0 /. 12.0
  | Two(Biased_dice)   -> 2.0 /. 12.0
  | Three(Biased_dice) -> 3.0 /. 12.0
  | Four(Biased_dice)  -> 1.0 /. 12.0
  | Five(Biased_dice)  -> 1.0 /. 12.0
  | Six(Biased_dice)   -> 4.0 /. 12.0

Given the above definitions, we can now form various events.

Sum-event

I call an event a sum-event when it is a subset of the probability space $\Omega$ which is the set containing all the primitive elements. For example, consider the event when tossing a biased dice, the outcome is either 3, 5, or 6. Let’s call this event a. For simplicity, we can use list to represent a set:

1
let a = [Three(Biased_dice); Five(Biased_dice); Six(Biased_dice)]

The probability space itself can be represented as:

1
let omega_biased = [One(Biased_dice); Two(Biased_dice); Three(Biased_dice); Four(Biased_dice); Five(Biased_dice); Six(Biased_dice)]

Using a plain list to represent a set, we have to be careful not to have duplicate entries, and it does not support union and intersection operations automatically. A better way is to use a proper set library such as Core.Set.

Now we can define the probability function for the probability space of dice tossing.

1
2
3
4
5
let prob_fair event =
  List.fold ~f:(fun x y -> x +. prob_fair_elem y) ~init:0.0 event
let prob_biased event =
  List.fold ~f:(fun x y -> x +. prob_biased_elem y) ~init:0.0 event

The above two functions simply sum the probabilities of each of the elements in an event. For example, for event a, its probability is

1
(prob_biased_elem Three(Biased_dice)) +. (prob_biased_elem Five(Biased_dice)) +. (prob_biased_elem Six(Biased_dice))

It can be verified that they satisfy the two requirement for $P$. In programming language theory, the types toss and fair_dice are called sum types.

Come back to the $\cap$ operator, for sum-events, $\cap$ means intersection, this is because the result of tossing a dice can only have one value. Two events can both happen only when they share some common elements. Sum- events can not be independent, since occurrence of one value means other values are excluded.

Product-event

Suppose we wish to study the probability of tossing both a fair dice and a biased dice. For example, we can ask what is the probability that fair dice has value 3 and biased dice has value 6. Starting again from the definition of probability space, we can first ask what the primitive elements are. Clearly we can use an ordered pair $(x, y)$ to record the outcomes, where $x$ is the result of tossing the fair dice, $y$ is the result of biased dice. Since each of the dice has six faces, there are $6\times 6 = 36$ such ordered pairs. Next we can ask what probability we shall assign to each such pair. The answer is the product of the probabilities of each dice. The reason is that among all the outcomes, there are $P(x)$ of chance to get $x$ for the fair dice, and among the all the outcomes of tossing the two dice with the fair dice having a value $x$, the probability is $P(y)$. This is essentially the multiplication rule for counting outcomes of an experiment. So new treating these ordered pair as building blocks, we can proceed to construct probability function and events.

In OCaml, such an ordered pair can be nicely represented as a tuple, e.g., (Three(Fair_dice), Six(Biased_dice)). Because these new building blocks have much richer internal structures, they have more interesting properties. A general event in these two-dice space looks like [(Five(Fair_dice), Four(Biased_dice)); (One(Fair_dice), Six(Biased_dice))], which is simply a set (list) of ordered pairs. However, if examine them closely, it is easy to see that we can at least classify them into two classes of sets.

  • Events for the fair and biased dice are independent
    For this class of events, we can always represent them as a product of the event by tossing fair dice and that of the biased dice. One example:
    1
    let two_dice_event = ([Two(Fair_dice); Three(Fair_dice)], [One(Biased_dice); Five(Biased_dice); Six(Biased_dice)])

OCaml will report the type of it is val two_dice_event : fair_dice toss list * biased_dice toss list. This is an example of product type. As for sum-event, we can call such an event product-event. Consider again $\cap$ operator, if we have an event $A$ for fair dice, and an event $B$ for biased dice, the event $A\cap B$ actually means forming a product-event, and we have $P(A\cap B) = P(A)P(B)$, meaning $A$ and $B$ are independent events.

  • There is a relation or constraint between the events of fair and biased dice
    For example, the event where the sum of the face values when tossing the two dice is 5:

    1
    let sum_five = [(Two(Fair_dice), Three(Biased_dice)); (Three(Fair_dice), Two(Biased_dice)); (One(Fair_dice), Four(Biased_dice)); (Four(Fair_dice), One(Biased_dice)]

    Such an event cannot represented as a product of fair dice event and biased dice event, it is a sum-event with a constraint.

After I used computer programs to solve probability problems, I used to implicitly use these concepts without realizing them. Programming using a good typed language forced me to think more clearly. And doing so actually helped me to understand both probability and programming better.